三角形だと底辺×高さ÷2なのに、台形だと上底+下底ってなるのか。 何年の学習指導要領で小中学校を過ごしてきたのだろう。 一時期台形の面積がなかった時期があったと記憶している。 台形を対角線で切り離す。面積は2つの 三角形の和だ。 (上底下底)×高さ÷2 = 上底×高さ÷2+下底×高さ÷21/2 小学校6 年生 算数 面積 <三角形の面積> 高さ 底辺に垂直な直線ad 公式: 三角形の面積 = 底辺 ×2 = 6 c m 2 と求められます。 上図のように

二等辺三角形や台形の面積と三平方の定理 中学3年数学 Youtube
底辺×高さ÷2 台形
底辺×高さ÷2 台形-2 ● 円の公式 円の面積 半径×半径×3.14 円周 底辺×高さ÷2ってのは 三角形の面積の式ですから直角三角形にこだわる必要はありませんよ 対角線を一本引いてみてください すると底辺をa、高さhの三角形と、底辺をb、高さhの三角形の二つに切ることができるでしょ 底辺aの三角形の面積はah/2 底辺bの三角形の面積はbh/2 二つの




台形の面積 数学が嫌いなんです
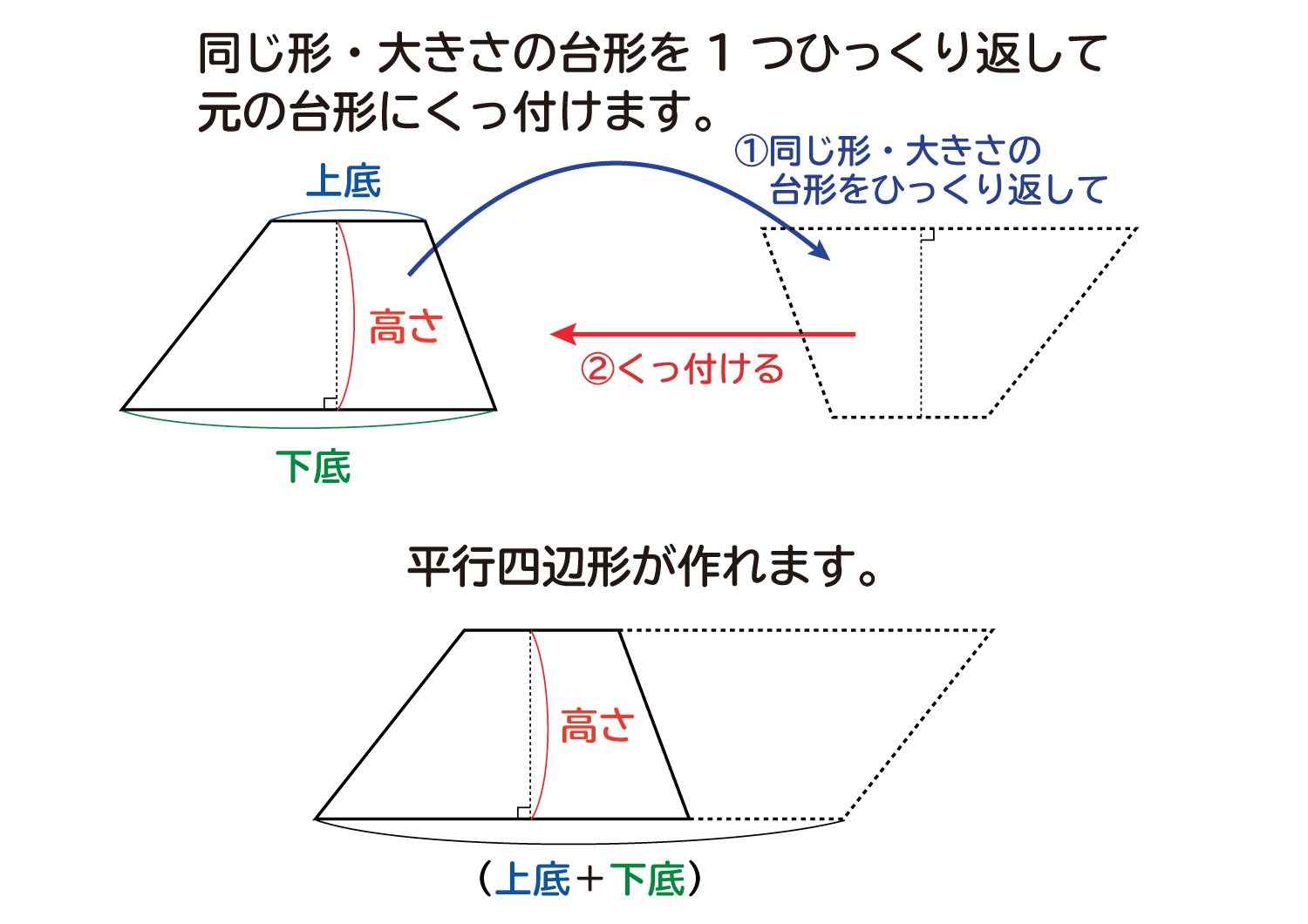
3=12 ではなく、 4 ×台形を2つ合わせた平行四辺形の面積=(上の辺十下の辺)×高さとなる。 台形の面積は,この平行四辺形の面積の半分なので, 台形の面積=(上の辺+下の辺)×高さ÷2 となる。上の図で台形の面積は, (3+6)×4÷2=18で,18c㎡である。 trsF2tmpjtd 岩倉市2=6 になります。 図2 (2) 高さは必ず底辺に垂直(直角)な線で測らなければなりません。
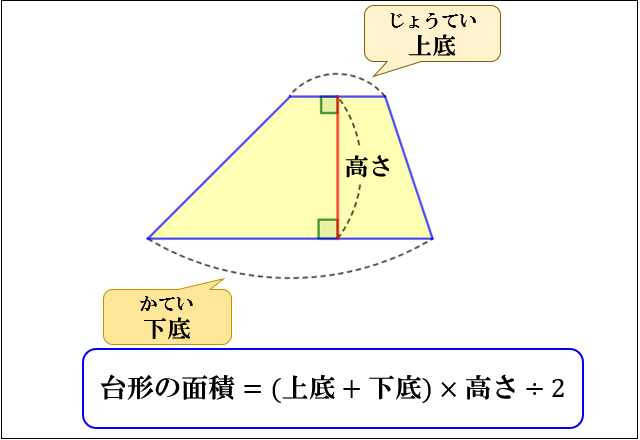
・ 三角形の面積=底辺×高さ÷2 ・ 平行四辺形の面積=底辺×高さ ・ 台形の面積=(上底+下底)×高さ÷2 ・ ひし形の面積=対角線×対角線÷2高さ 三角形の面積 = 底辺 ×なので, 台形の面せきは, たての長さ×よこの長さ で四角形の面せきを出してから, 2でわります。 ( 上辺 + 底辺 )×
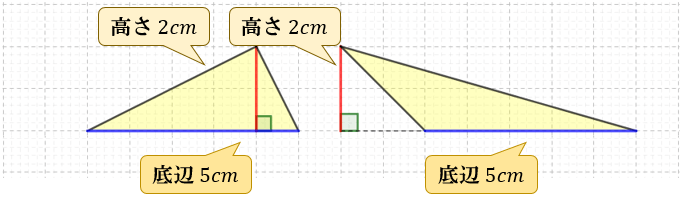
16×11÷2=(㎠) 答え ㎠ 問題⑤ 面積が63㎠である、次の三角形の高さを求めましょう。 《三角形の高さの求め方》 この三角形の底辺の長さは9cm、高さは cm、面積は63㎠なので、これらを三角形の面積を求める公式に当てはめます。 すると よって前号に続いて台形の面積公式 その2です(^_^)。 本文に入る前に、台形の面積=(上底+下底)×高さ÷2を説明するもう一つの方法があることをお伝えしておきたいと思います。 平行四辺形の面積公式はご存じと思いますが底辺×高さです。底辺×高さ÷2で①の面積を求めることができます。 鋭角三角形 下図の様に補助線を引きます。 鋭角三角形は直角三角形が二つあると考えると分かりやいです。 鈍角三角形 このような鈍角三角形の面積は「底辺×高さ÷2」で説明できるのでしょうか。



三角形と台形の面積



Q Tbn And9gcskqz Ppdvuumkcspdfklsb3r C5mohfuqvemohgl8suerhw5lr Usqp Cau
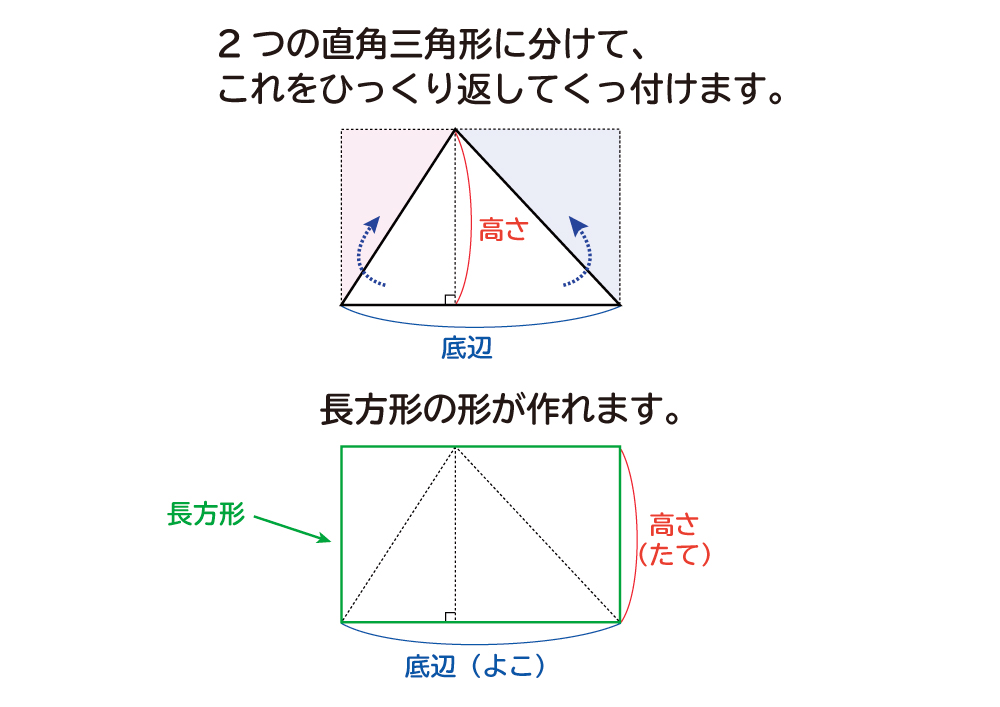
長方形の面積は「たて×よこ」で求めることができるので、この長方形を作った元の三角形の面積は半分の「底辺×高さ÷2」で求めることができます。 ぴよ校長 三角形を2つ使うと、長方形の形を作る ことができたね! これとは別の方法でも、三角形の面積の公式の確認することができます。 先ほどの三角形を下の図のようにひっくり返して、くっ付けます。 する2 問題:三角形の面積を求めましょう。 ① ② <平行四辺形の面積> 問題:平行四辺形の面積をまとめましょう。基本1 (2) 台形の面積の公式は,「(上底+下底)×高さ÷2」です。 右図で,上底は5cm,下底は cm,高さは8cmです。 台形の面積は56cm2であることが問題に書いてありましたから, あとは逆算をするだけです。 14-5=9(cm) 基本1 (3)



2 Abef Cm Descubre Como Resolverlo En Qanda



至急です 台形の面積って 上辺 下辺 高さ 2で出しますよね 他に台形 Yahoo 知恵袋
台形の面積の公式 (上底+下底)×高さ÷2=台形の面積 じょうてい たす かてい かける たかさ わる2 ひし形の面積の公式 対角線×対角線÷2=ひし形の面積 たいかくせん かける たいかくせん わる2● 面積の公式 平行四辺形の面積 底辺 ×その時の高さはもう一方の対角線の長さの半分になっています。 対角線①⇒底辺 対角線② ÷2 ÷



2 Abef Cm Descubre Como Resolverlo En Qanda




二等辺三角形や台形の面積と三平方の定理 中学3年数学 Youtube
台形は三角形二つからなっています。 ですので、 上底×高さ÷2+下底×高さ÷2=台形の面積で、 (上底+下底)×高さ÷2 という公式が完成します。 1人 がナイス!2 」 という公式から求めることができます。 例題:底辺 4 c m 、高さ 3 c m の三角形の面積を求めてください この問題では 公式 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 ×三角形の面積=底辺×高さ÷2 台形の面積=(上底+下底)×高さ÷2 高さ ひし形の面積=一方の対角線×もう一方の対角線÷2



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
2 ⇒高さ 平行四辺形の面積は『底辺×高さ』なので、元のひし形の 『対角線×対角線÷2 ÷2 台形の面積 点D を点A に近づけて重ねると 三角形の面積 台形の上底を cm とみることで,台形の公式を使って三角形の面積を高さ 三角形の面積 底辺 ×




台形の面積の公式 ゆとり教育で求め方がわからない人は見て 中学や高校の数学の計算問題




台形の面積の求め方 公式と計算例
台形の底辺と計算(求め方)、上辺の関係 台形の底辺は、 高さ 面積 上底(または下底) が既知のとき計算できます。これは台形の面積を求める式が、 台形の面積=(上底下底)×高さ÷2 のためです。実際に、下図の台形の底辺(下底)を計算します。平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷2 台形の面積= (上底+下底)×高さ÷2 三角形の面積=底辺×高さ÷2 円の面積=半径×半径×円周率 (314) おうぎ形の面積=半径×半径×円周率×中心角/360°平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷2 台形の面積=(上底+下底)×高さ÷2 ※台形の面積は特に忘れやすいので注意が必要です。 正方形はひし形でもあるので 正方形の面積=対角線×対角線÷2 でも求められることも覚えておくといい




底辺 Wikipedia




Descubre Como Resolverlo En Qanda
2 』 がひし形の面積になるのです。 ちなみに平行四辺形の面積が『底辺×高さ』になる理由はこちらにまとめています。 平行四辺形の面積の公式|なぜ『底辺×高さ』で求め2 」 に当てはめて 面積 面 積 = 4 ×1 台形の面積 算数の公式。5年生で習うらしい。 台形の面積=(上底下底)×高さ÷2 大人になった今となってはクイズ番組で聞かれるくらい。こんなものを教科書の太字にされていたら、数学は役に立たないと言われても仕方ないよ。 2 数学の思考の本質 僕が思う数学を勉強する意味がある。




台形の任意の高さにおける上辺の長さ 相似関係の2つの台形の高さがそれぞれ Okwave



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
2 ひし形の面積 対角線 ×また、「ひし形」は 平行四辺形の一種でもありますので、「底辺」×「高さ」でも求められること も忘れないようにしておきましょう。 3 「台形」 「(上底下底)×高さ÷2」で求められる公式をまずはしっかりといつでも取り出せる ようにしましょう。これミズキ そうすると、底辺は6㎝2㎝で8㎝。 ミズキ それじゃ、カイちゃん、黄色の台形の面積は? カイト 黄色の台形の面積は、平行四辺形の面積の半分。 ミズキ 正解です。 ミズキ 台形の面積の公式は「上底下底×高さ÷2」となります。




四角形と三角形の面積



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル
2 = 台形の面せき ×平面図形の面積の求め方の公式 ■多角形の面積の求め方 長方形=縦×横 正方形=1辺×1辺=対角線×対角線÷2 平行四辺形=底辺×高さ 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積三角形の底辺が3、高さ4、三角錐の高さが5のとき 三角錐の体積=3×4÷2×5÷3=10cm 3 です。 まとめ 今回は体積の公式について説明しました。体積の公式は色々あると思いがちですが、基本の公式は「底面積×高さ」「底面積×高さ÷3」です。



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
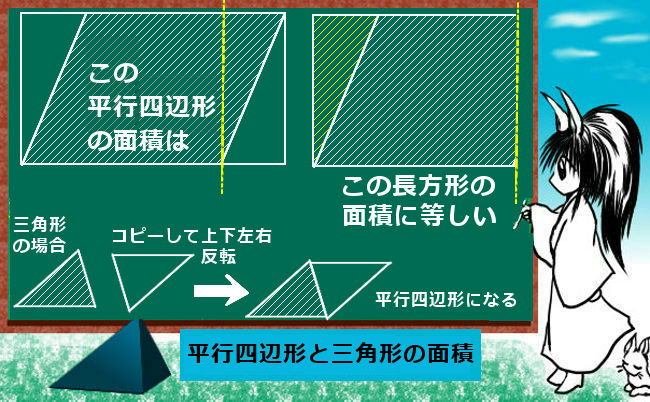



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori
三角形の面積=底辺×高さ÷2 1 台形の面積 台形では,平行な2辺のいっぽうを上 じょう 底 てい , もういっぽうを下 か 底 てい といいます。 また,上底と下底の間の垂直な直線の長さ を高さといいます。 台形の面積=(上底+下底)×高さ÷2 2 ひし形の面積三角形の面積は 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 ×平行四辺形の面積 = 底辺 ×
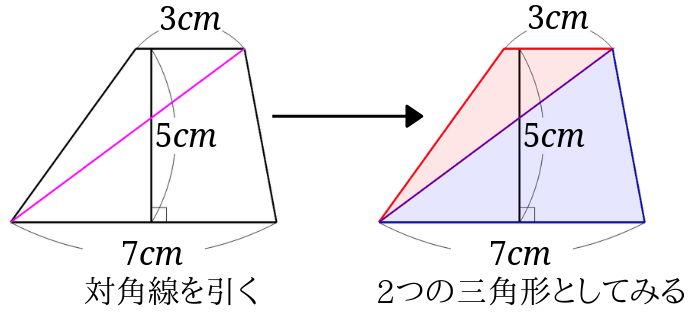



台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校
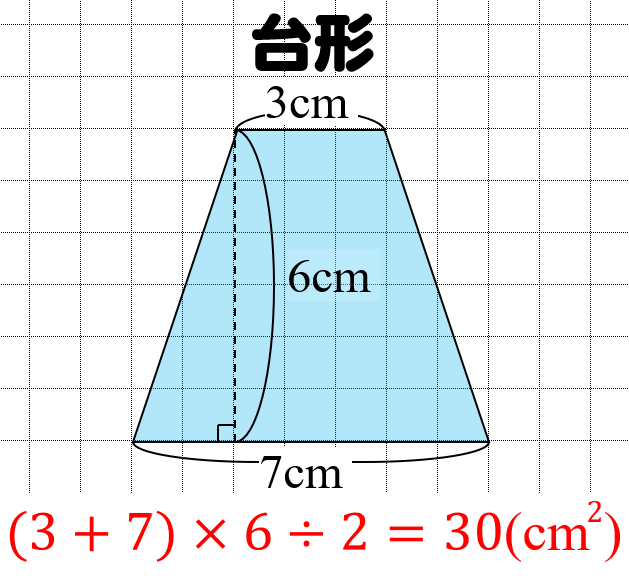



台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
底辺×高さ÷2ってのは 三角形の面積の式ですから直角三角形にこだわる必要はありませんよ 対角線を一本引いてみてください すると底辺をa、高さhの三角形と、底辺をb、高さhの三角形の二つに切ることができるでしょ 底辺aの三角形の面積はah/2 底辺bの三角形の面積はbh/2 二つの和がこの台形基本2 台形の面積は,「(上底+下底)×高さ÷2」で求めることができます。 上底は6cm,下底はわかっていないので cmとし,高さは8cm,面積は68cm2ですか ら, 17-6=11 よって,辺BCの長さである cmは,11cmになります。平行四辺形の面積=底辺×高さ÷2 ですね。この問題の場合,高さが与えられていない代わりに,底辺以外の辺とその挟む角が与えられています。よって,この2つのことがらより高さ h を求めることにし




平行四辺形の面積の求め方 公式と計算例
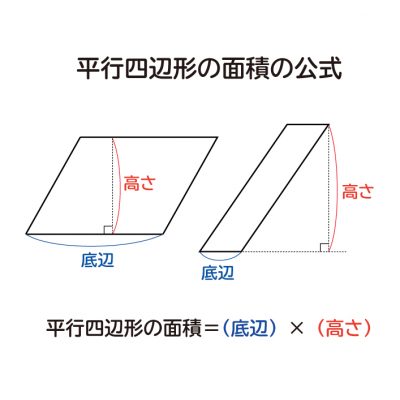



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル
この平行四辺形の面積は『底辺×高さ』で求めることができ、底辺は元の台形の(上底下底)にあたります。 そして平行四辺形は 求める台形の2つ分の大きさなので、台形の面積は『(上底下底)×高さ÷2 ÷そしてその平行四辺形の面積(=(底辺)×(高さ))は (a b) h であり、その半分が台形の面積にあたるので S = (a b) h /2 が導かれる。 a = 0 とおくと底辺 b の三角形の面積に等しい。




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




小学5年生 ひし形 台形の面積 算数 Active Learning 学院



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
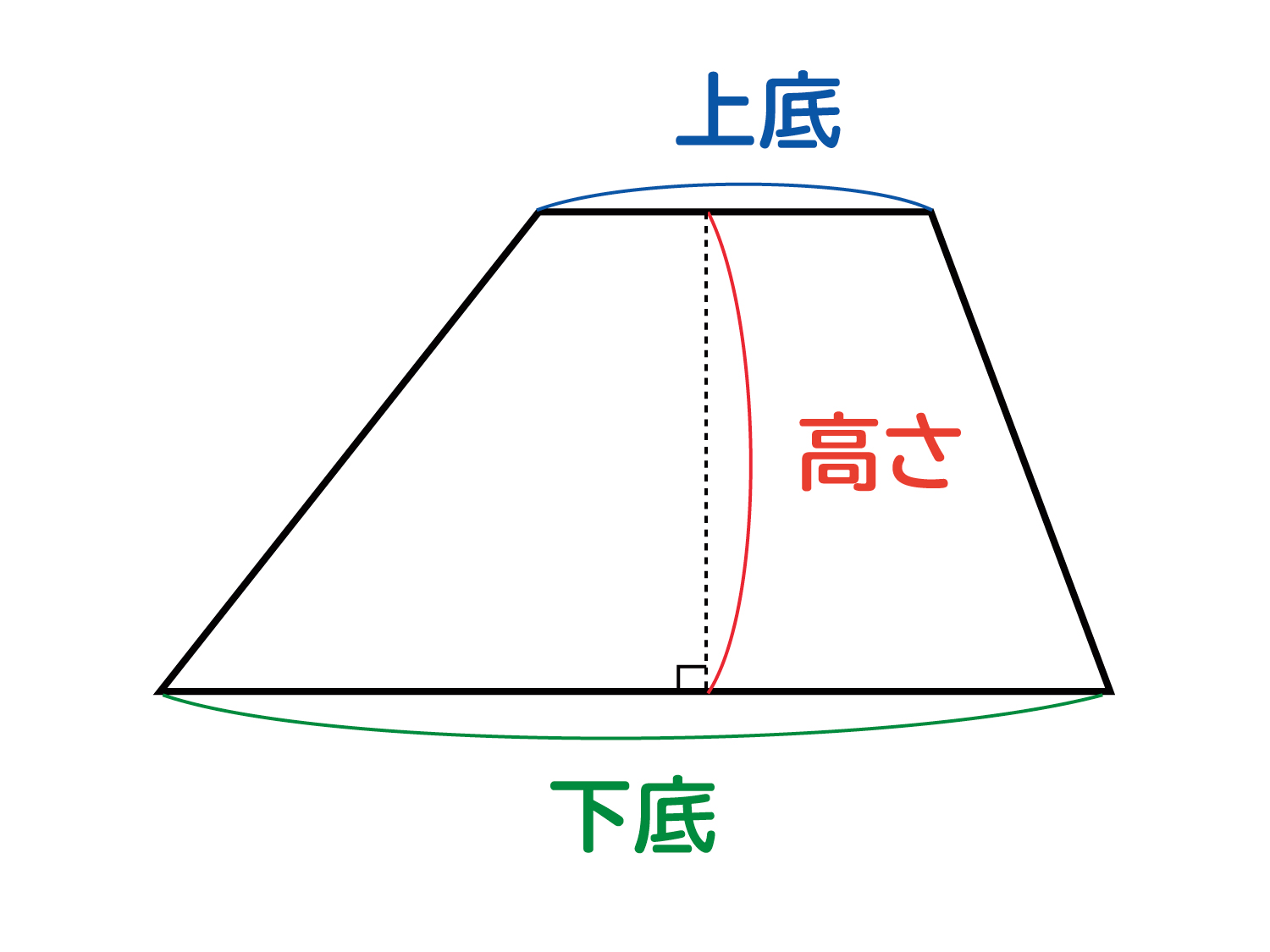



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル




面積の公式 Youtube




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法
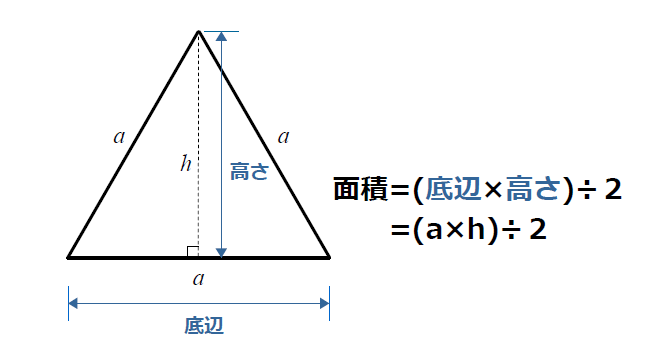



正三角形の面積計算 ゆるゆるプログラミング



なぜ三角形は底辺 高さ 2なのですか どうして 2がはいるのです Yahoo 知恵袋




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校




台形の面積の求め方 公式と計算例



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
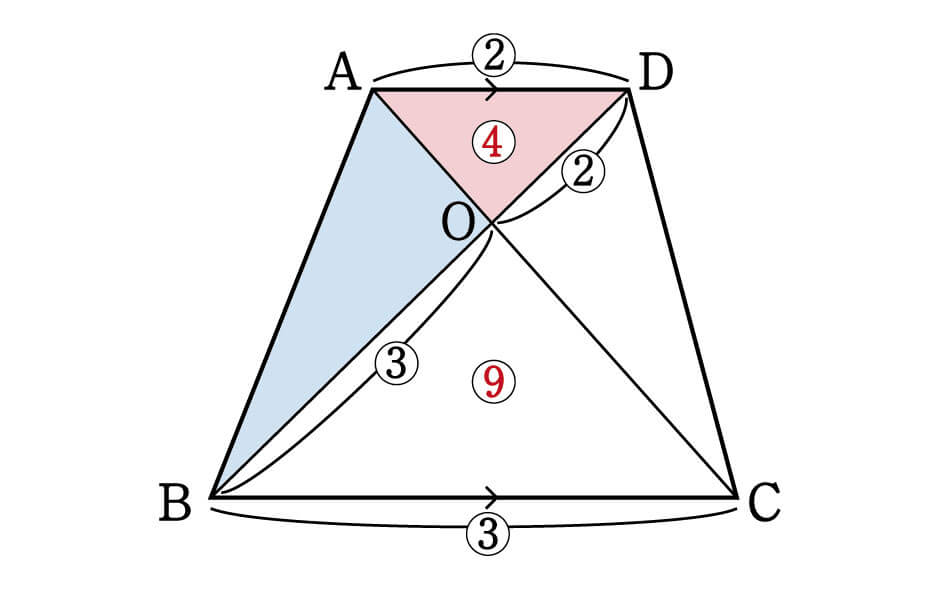



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




相似 台形と面積比の問題を徹底解説 数スタ



Www Chuo Tky Ed Jp Ginza Jh Resources Content 9998 0416 Pdf




仕事で 高さの分からない台形の面積を求めないといけません 仕事で 数学 教えて Goo




平行四辺形の面積の求め方 公式と計算例




三角形の面積って 底辺 高さ 2 ではありませんでしたか それとも今回 数学 教えて Goo



台形の底辺は 1分でわかる意味 計算 求め方 上辺 面積との関係



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



Www City Ota Tokyo Jp Kyouiku Topics Syougakuseigakusyu Files Gonensansuukaisetu Pdf



底辺6cm高さ8cmの直角三角形を高さの1 2のところで切り取 Yahoo 知恵袋
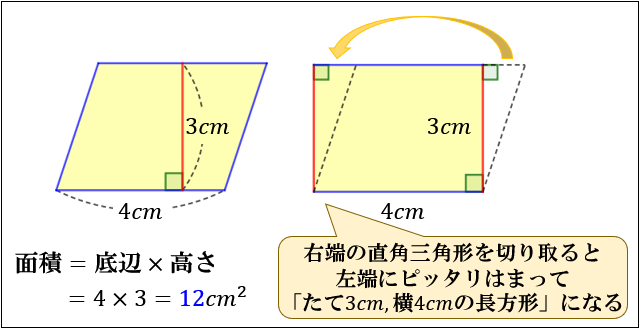



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
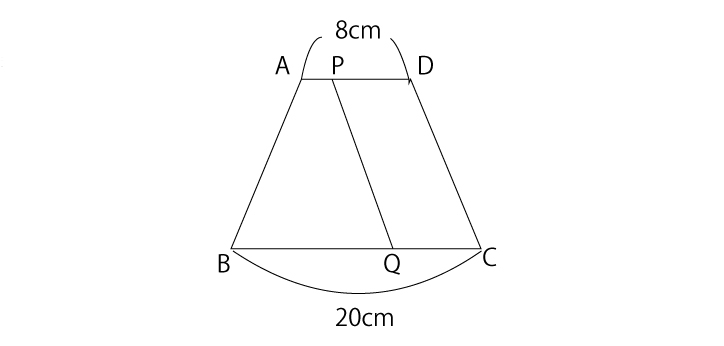



台形の面積公式 暗記よりも理解が大事 応用が利く図形問題の考え方 中学受験ナビ




ベスト底辺高さ2 英語 最高のぬりえ



台形の底辺は 1分でわかる意味 計算 求め方 上辺 面積との関係



台形上辺 300 底辺 高さ 1500 五分の勾配これで底辺と Yahoo 知恵袋
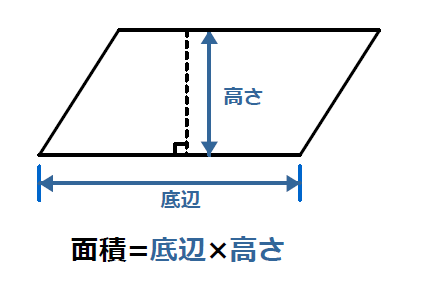



平行四辺形の面積計算 ゆるゆるプログラミング




台形の 面積 底辺 角度 から上辺 高さを計算したい その2 先 数学 教えて Goo



1
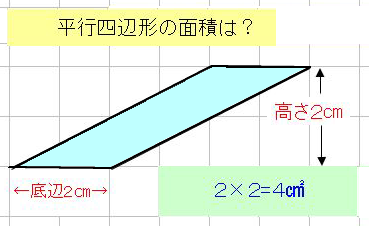



5年算数面積2 教え方のポイント




数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
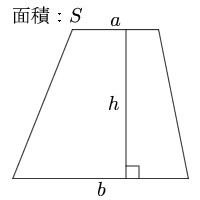



台形 面積の計算 計算サイト




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
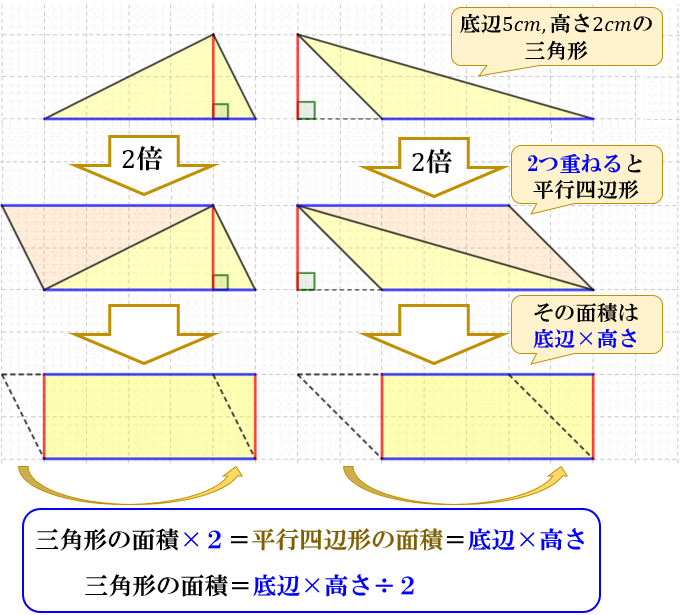



無料ダウンロード底辺高さ2 証明 最高のぬりえ



5年算数面積2 教え方のポイント
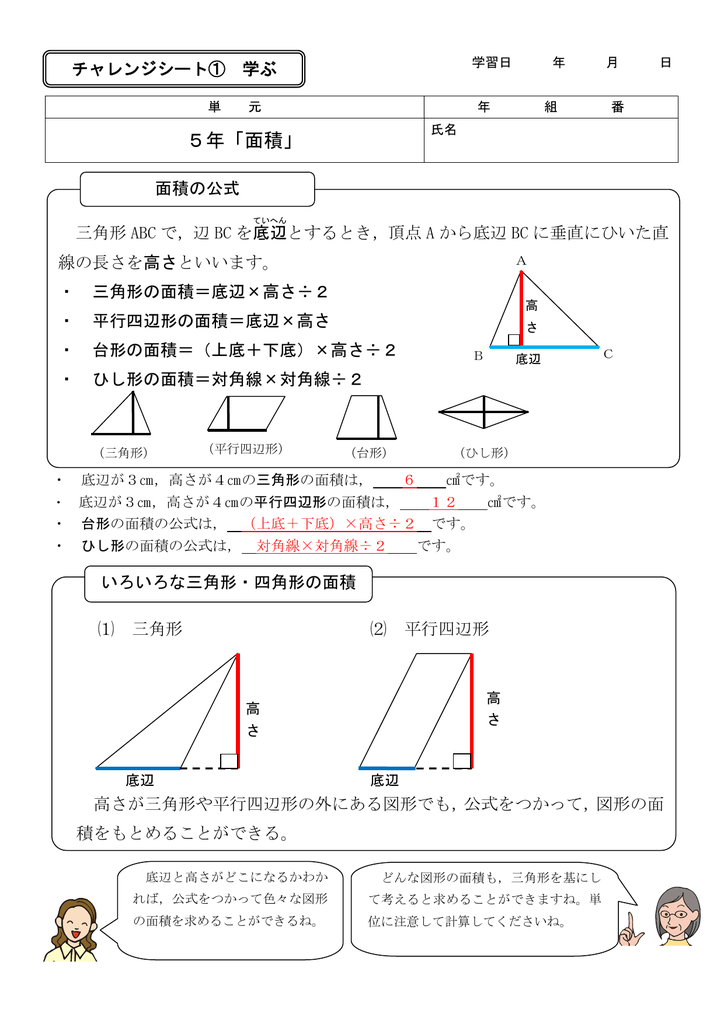



5年 面積



5年算数面積2 教え方のポイント
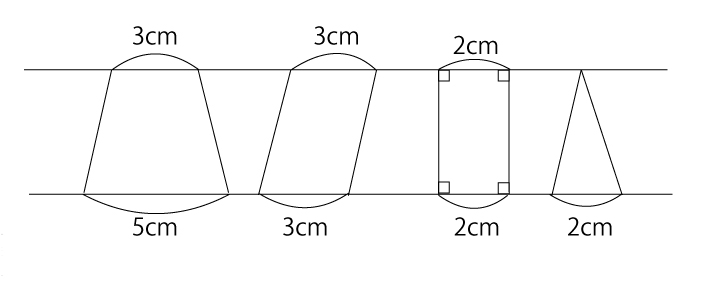



台形の面積公式 暗記よりも理解が大事 応用が利く図形問題の考え方 中学受験ナビ




平行四辺形の面積の求め方 公式と計算例




台形の面積の求め方 公式と計算例




小学生は算数が好きなる 小学生の算数 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト
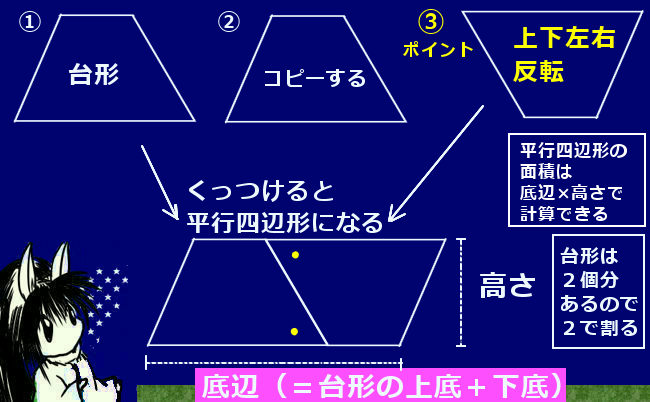



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori




台形の面積 数学が嫌いなんです




面積の求め方 算数の教え上手 学びの場 Com




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
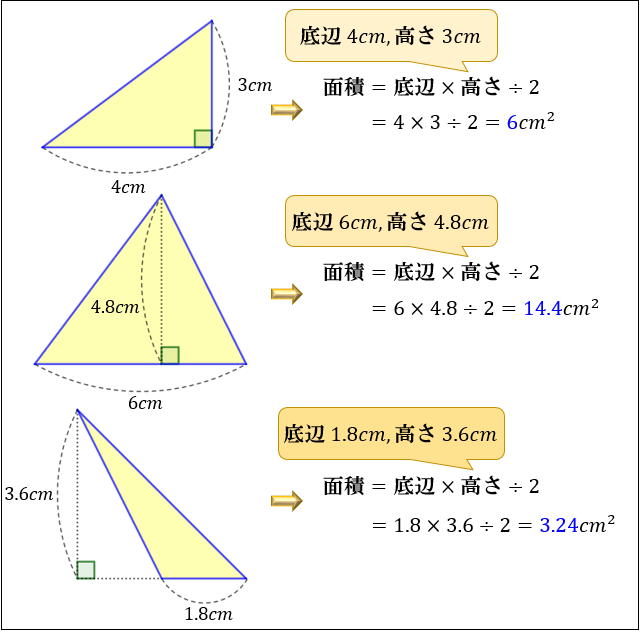



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
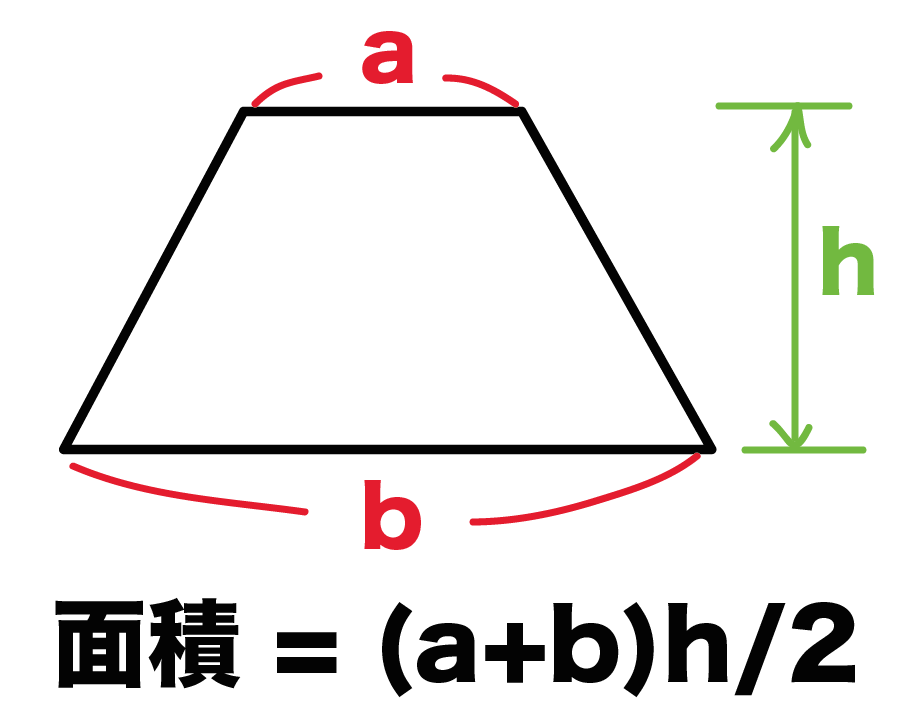



高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




台形の面積の求め方 公式と計算例
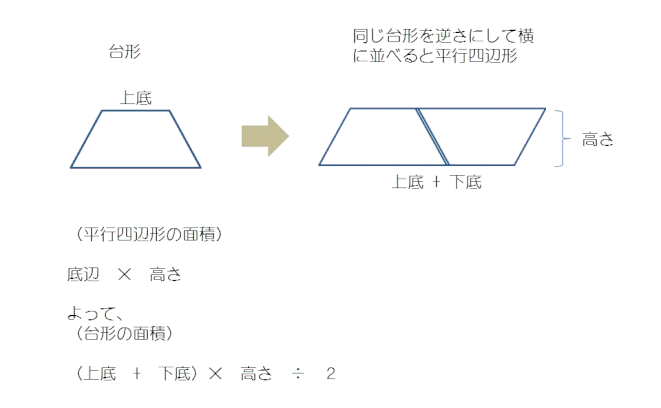



台形の面積の公式は柔軟な思考で覚えるようにすること 小学生の子供の成績を上げる方法




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



Http Www Pref Osaka Lg Jp Attach 6629 H Emw 5b1 1 5 7 Pdf



2
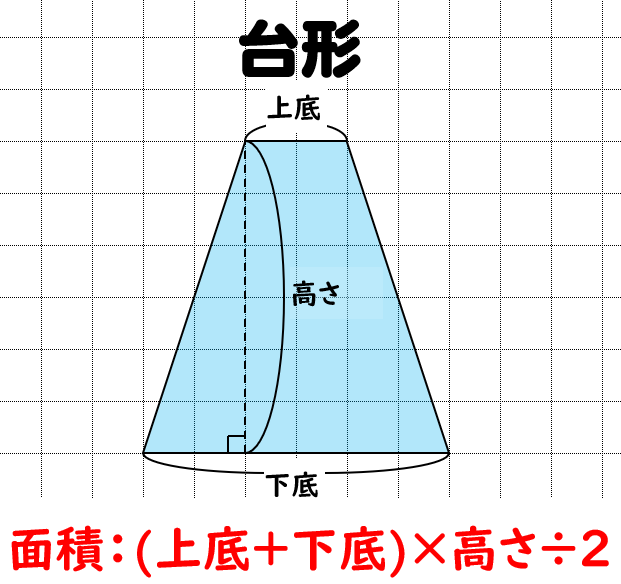



台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
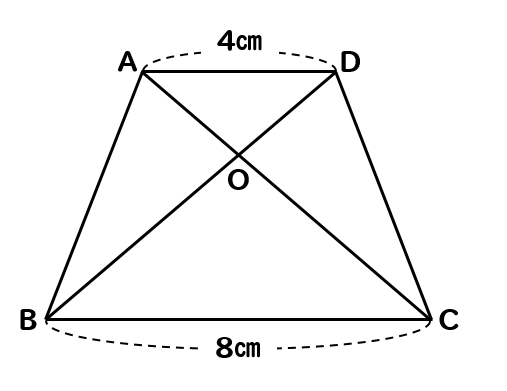



相似 台形と面積比の問題を徹底解説 数スタ
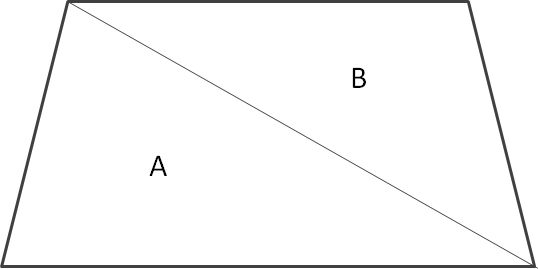



台形の面積の計算機 二等分 求め方 Nujonoa Blog



高さがわからない台形の面積の求め方を教えてください 高さがわか Yahoo 知恵袋



1
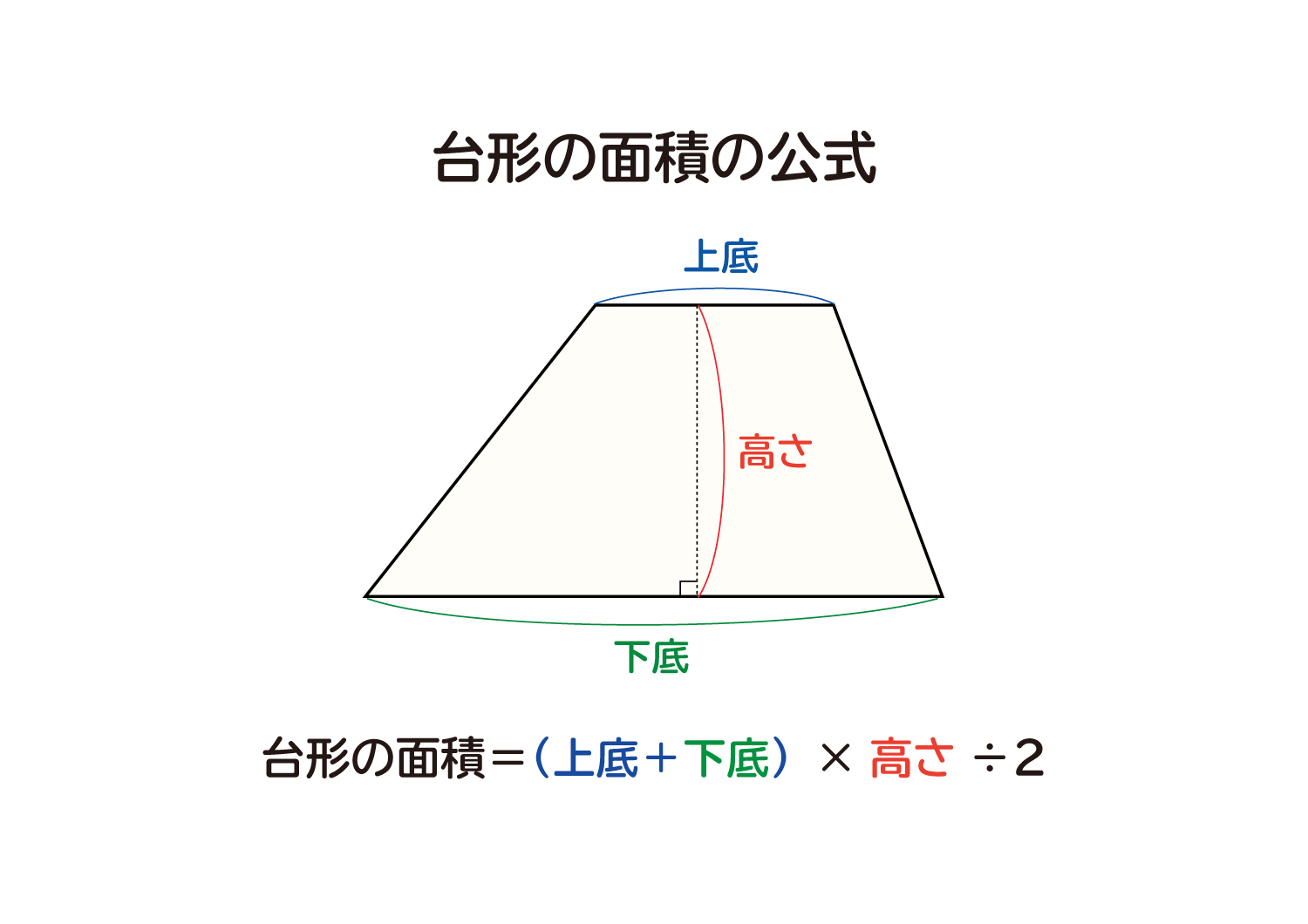



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル



台形 Wikipedia




台形の 面積 底辺 角度 から 上辺と高さ の求め方 台形の面積 数学 教えて Goo




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




台形の面積の求め方 公式と計算例




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




数学 好きになる Com 台形の面積




台形の面積を求める方法 8 ステップ 画像あり Wikihow



算数 テーマ別 ポイント集 平面図形 10 14 中学受験の勉強法 偏差値アップの学習法
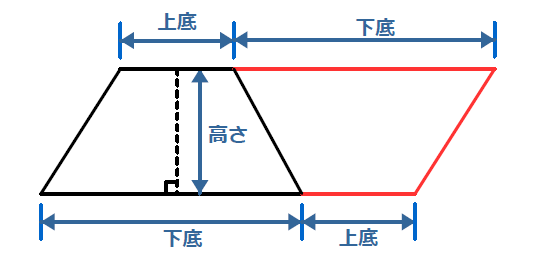



台形の面積計算 ゆるゆるプログラミング




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう
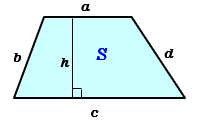



台形の1辺 面積 3辺の長さと高さから 高精度計算サイト



1
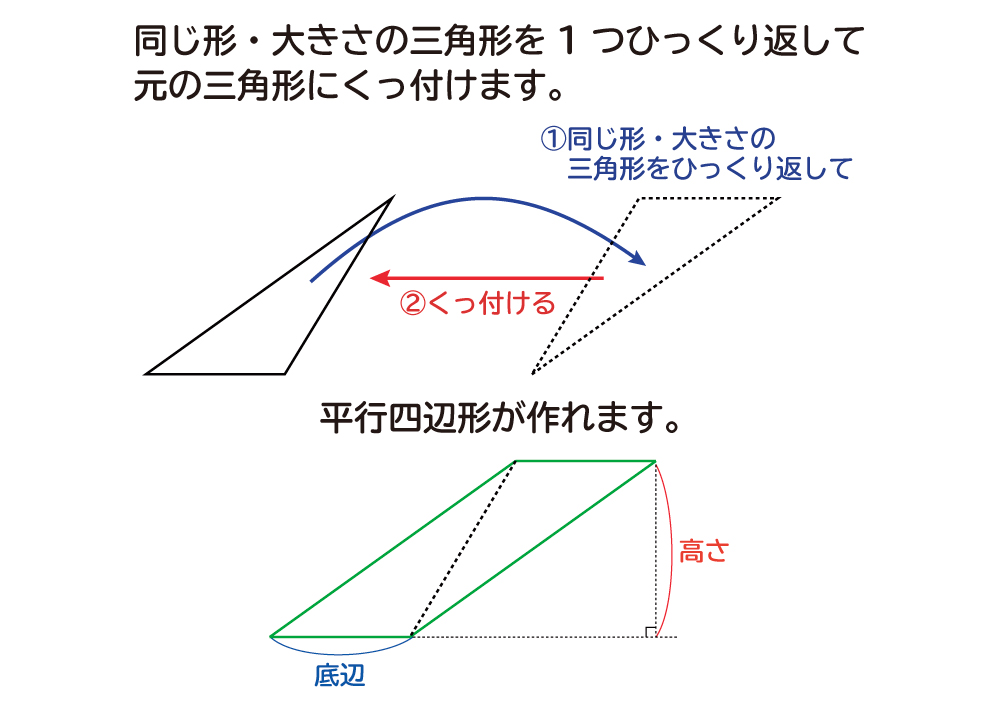



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
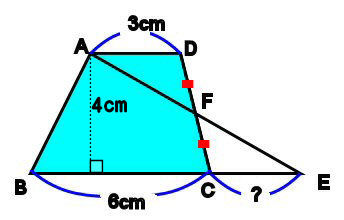



台形と三角形
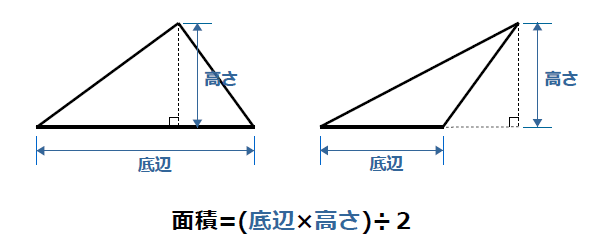



三角形の面積計算 ゆるゆるプログラミング



5年算数面積2 教え方のポイント




5年算数面積2 教え方のポイント
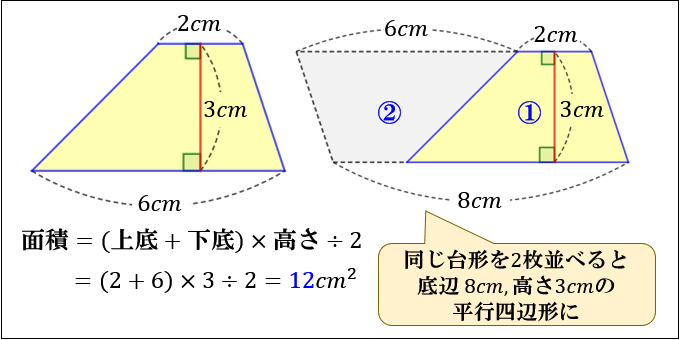



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
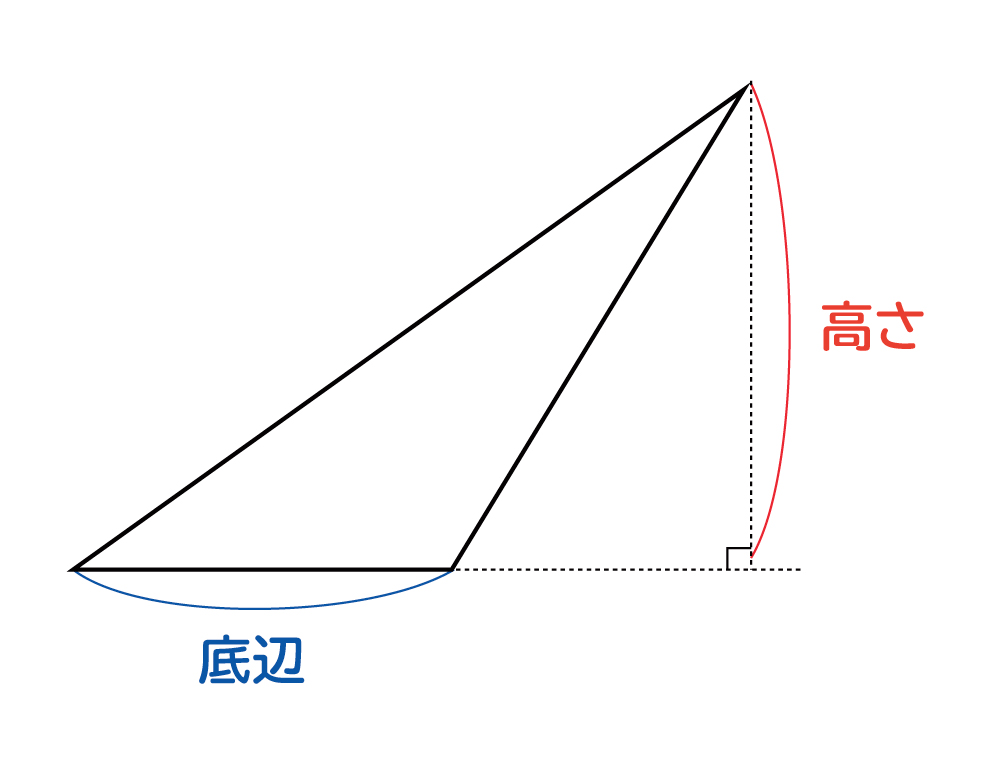



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル



0 件のコメント:
コメントを投稿